Tam Giác Có 2 Cạnh Bằng Nhau Là Tam Giác Gì? Định Nghĩa và Tính Chất

Tam Giác Có Hai Cạnh Bằng Nhau Là Tam Giác Gì?

Tam giác có hai cạnh bằng nhau được gọi là tam giác cân. Trong lĩnh vực hình học, loại tam giác này mang trong mình sự thú vị riêng nhờ vào các tính chất đặc biệt của nó. Nếu bạn là một người yêu thích toán học hay đơn giản chỉ muốn khám phá thêm về các khái niệm hình học, đọc tiếp để cùng tìm hiểu về lý thuyết này.

Tam Giác Cân Là Gì? Định Nghĩa và Tính Chất

Nói một cách đơn giản, tam giác cân là một dạng đặc biệt của tam giác, trong đó có hai cạnh bằng nhau. Thường thì, khi nhắc đến tam giác cân, hai cạnh này được gọi là cạnh bên, và đỉnh đối diện với cạnh đáy là góc đỉnh. Một điều quan trọng nữa là hai góc ở đáy của tam giác cân luôn bằng nhau. Vì vậy, tam giác cân không chỉ dễ nhận biết mà còn mang lại cho chúng ta một số tính chất thú vị.

Dấu Hiệu Nhận Biết Tam Giác Cân

Khi nhắc đến đặc điểm nhận diện của tam giác cân, việc quan sát các cạnh là hết sức quan trọng. Một tam giác mà có hai cạnh bằng nhau đương nhiên là một tam giác cân. Cũng không thể bỏ qua những góc nằm trên đáy, chính sự bằng nhau của hai góc này cũng là một chỉ dấu mạnh mẽ xác nhận rằng bạn đang đối diện với một tam giác cân .

Cách Tính Diện Tích Tam Giác Cân

Một trong những cách để thể hiện sự hiểu biết của mình về tam giác cân, chính là tính toán được diện tích của nó. Để tính diện tích tam giác cân với cạnh đáy là b và chiều cao là h, ta có công thức S = 1/2 b h. Lấy một ví dụ đơn giản, nếu chiều dài cạnh đáy b là 6 và chiều cao từ đỉnh xuống đáy là 3, thì diện tích sẽ là 9. Đây chỉ là một đoạn ngắn giúp bạn nắm rõ cách tính diện tích. Còn nhiều ứng dụng khác mà chắc chắn bạn sẽ muốn học hỏi.

Phân Biệt Tam Giác Cân và Tam Giác Đều

Mặc dù cả tam giác cân và tam giác đều đều có yếu tố "cân bằng" trong cấu trúc của chúng, sự khác biệt giữa hai dạng này khá rõ ràng. Tam giác đều là một tam giác mà cả ba cạnh và ba góc đều bằng nhau. Ngược lại, tam giác cân chỉ yêu cầu hai trong số ba cạnh và hai góc ở đáy bằng nhau. Hiểu được điều này sẽ giúp bạn không bị nhầm lẫn khi làm bài hoặc áp dụng kiến thức vào thực tế .

Ứng Dụng Của Tam Giác Cân Trong Toán Học

Ngoài các tính chất đáng chú ý, tam giác cân còn xuất hiện thường xuyên trong nhiều bài toán khác nhau, từ hình học phẳng đến không gian. Nó cũng được dùng để chứng minh nhiều định lý hình học quan trọng. Ví dụ, trong việc xác định một hình vuông, ta sẽ cần chứng tỏ rằng hai đường chéo có độ dài bằng nhau. Bằng cách thực hiện cắt một tam giác vuông tại điểm giữa của cạnh dài, bạn vô tình sẽ tạo ra một tam giác cân, giúp làm sáng tỏ bài toán.

Bài Toán Thực Tế Về Tam Giác Cân

Một ví dụ đơn giản là việc tính toán chiều cao của một cây dựa trên bóng của nó ở mặt đất. Bằng cách xác định tam giác cân được tạo ra giữa cây và bóng, bài toán trở nên dễ giải hơn nhiều. Việc đặt tam giác cân trong ngữ cảnh khả thi và thực tế không chỉ là một cách tuyệt vời để hiểu được giá trị của khái niệm hình học này mà còn là một cách để thông qua đó nhận biết môi trường xung quanh chúng ta .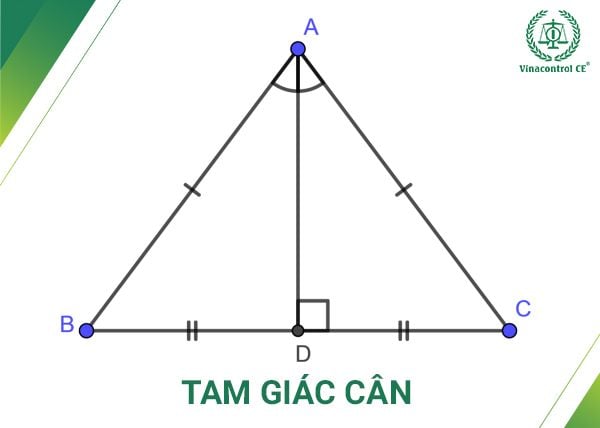

Câu Hỏi Thường Gặp Về Tam Giác Cân

Nếu bạn có bất kỳ thắc mắc nào về tam giác cân, dưới đây là một số câu hỏi phổ biến có thể bạn quan tâm:

• Làm sao để xác định một tam giác cân trong bài toán?
• Tam giác vuông cân có phải là một trường hợp đặc biệt của tam giác cân không?
• Những ứng dụng nào của tam giác cân bạn thấy đáng chú ý nhất?

Xin đừng ngần ngại để lại câu hỏi, thảo luận thêm về những vấn đề bạn thấy thú vị hoặc chưa rõ ràng.

Kết luận

Khám phá về tiếng vang của tam giác cân sẽ mang đến cho bạn một công cụ giải quyết vấn đề linh hoạt và sâu sắc. Đừng quên để lại bình luận để mình biết những chủ đề nào bạn muốn mình bàn luận thêm hoặc chia sẻ bài viết này nếu bạn thấy hữu ích. Hãy cùng kết nối và tìm hiểu thêm kiến thức tuyệt vời tại mncatlinhdd.edu.vn.

Nguồn: http://mncatlinhdd.edu.vn/ Tác giả: Nguyễn Lân dũng