Tâm Đối Xứng Đồ Thị Hàm Số Là Gì? A-Z Cách Xác Định & Ứng Dụng

1. Định Nghĩa Tâm Đối Xứng của Đồ Thị Hàm Số

Tâm đối xứng đồ thị hàm số là một điểm đặc biệt. Nếu ta lấy một điểm bất kỳ trên đồ thị và tìm điểm đối xứng của nó qua điểm này, điểm đối xứng đó cũng sẽ nằm trên đồ thị.

Nói một cách toán học, điểm I(a, b) là tâm đối xứng của đồ thị hàm số y = f(x) khi và chỉ khi, với mọi x, ta có:

f(x + a) + f(-x + a) = 2b

2. Tính Chất Quan Trọng Của Tâm Đối Xứng

Hiểu rõ tính chất tâm đối xứng đồ thị giúp ta dễ dàng xác định và ứng dụng nó trong giải toán.

• Hàm số lẻ: Nếu y = f(x) là hàm số lẻ, tức là f(-x) = -f(x), thì gốc tọa độ O(0, 0) chính là tâm đối xứng hàm số.
• Hàm số bậc ba: Với hàm số bậc ba y = ax³ + bx² + cx + d, tâm đối xứng của hàm số trùng với điểm uốn của đồ thị. Điểm uốn là điểm mà tại đó đồ thị chuyển từ lồi sang lõm (hoặc ngược lại). 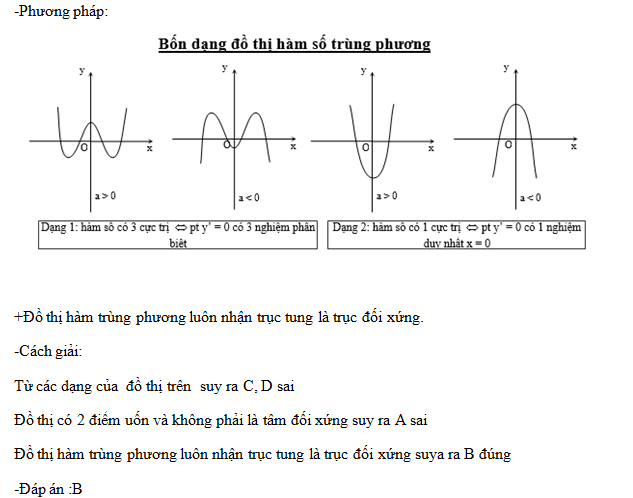Điểm uốn và tâm đối xứng có mối liên hệ mật thiết trong hàm bậc ba.

3. Phương Pháp Xác Định Tọa Độ Tâm Đối Xứng Đồ Thị Hàm Số

Để xác định tọa độ tâm đối xứng đồ thị, ta thực hiện các bước sau:

• Bước 1: Giả sử I(a, b) là tâm đối xứng của đồ thị hàm số y = f(x).
• Bước 2: Thực hiện phép tịnh tiến hệ trục tọa độ Oxy sang hệ IXY theo công thức:

  x = X + ay = Y + b

• Bước 3: Thay vào phương trình hàm số ban đầu, ta được phương trình mới:

  Y + b = f(X + a)

• Bước 4: Sử dụng điều kiện tâm đối xứng để tìm a và b. Biến đổi phương trình sao cho vế phải là một hàm lẻ của X. Khi đó, hệ số của các số hạng bậc chẵn (kể cả số hạng tự do) phải bằng 0. Giải hệ phương trình này, ta tìm được a và b.

4. Ví Dụ Minh Họa Cách Tìm Tâm Đối Xứng Đồ Thị Hàm Số

Ví dụ 1: Tìm tọa độ tâm đối xứng đồ thị hàm số y = x³ + 3x² – 9x + 1.

Giải:

1. Tính đạo hàm bậc nhất và bậc hai:
   • y’ = 3x² + 6x – 9
   • y” = 6x + 6
2. Giải phương trình y” = 0:
   • 6x + 6 = 0 => x = -1
3. Thay x = -1 vào hàm số ban đầu để tìm y:
   • y = (-1)³ + 3(-1)² – 9(-1) + 1 = 12

Vậy, tọa độ tâm đối xứng đồ thị là I(-1, 12).

Ví dụ 2: Tìm tâm đối xứng của hàm số y = x³ – 3x + 2.

Giải:

1. Tính đạo hàm bậc nhất và bậc hai:
   • y’ = 3x² – 3
   • y” = 6x
2. Giải phương trình y” = 0:
   • 6x = 0 => x = 0
3. Thay x = 0 vào hàm số ban đầu để tìm y:
   • y = (0)³ – 3(0) + 2 = 2

Vậy, tọa độ tâm đối xứng đồ thị là I(0, 2).

5. Ứng Dụng Thực Tế Của Tâm Đối Xứng

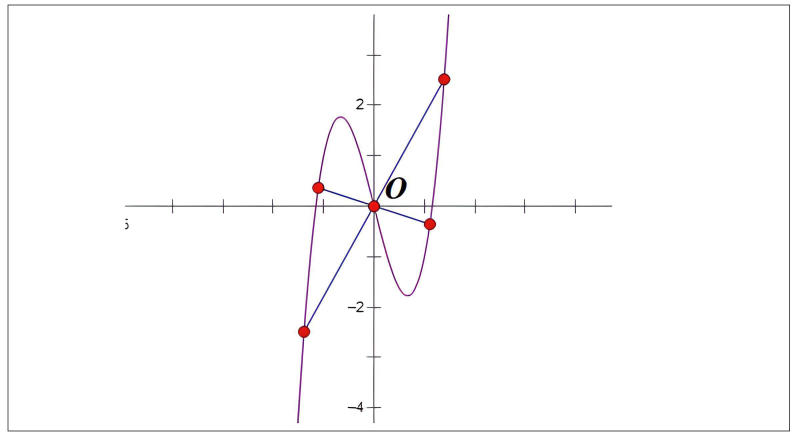Tâm đối xứng của đồ thị hàm số không chỉ có ý nghĩa trong toán học mà còn có nhiều ứng dụng thực tế. Nó giúp chúng ta hiểu rõ hơn về tính chất đối xứng của các đối tượng, từ đó ứng dụng vào:

• Thiết kế kiến trúc.
• Phân tích dữ liệu.
• Giải các bài toán tối ưu hóa.

6. Kết Luận

Việc xác định tâm đối xứng của đồ thị hàm số là gì và cách tìm nó là một kỹ năng quan trọng trong toán học. Nó giúp chúng ta nắm bắt được tính chất tâm đối xứng đồ thị và ứng dụng vào nhiều lĩnh vực khác nhau. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cơ bản và phương pháp xác định điểm đối xứng đồ thị hàm số một cách hiệu quả.

Nguồn: https://mncatlinhdd.edu.vn/ Tác giả: Nguyễn Lân dũng