Tâm Đối Xứng Của Đồ Thị Là Gì?

Curious about toán học và đặc biệt là việc nghiên cứu tính chất đối xứng của đồ thị không? Hôm nay, mình sẽ chia sẻ một khái niệm thú vị mang tên tâm đối xứng của đồ thị. Điều này không chỉ đem lại sự hiểu biết sâu rộng hơn về tính chất của hàm số mà còn có nhiều ứng dụng thực tế. Trong bài viết này, chúng ta sẽ khám phá mọi góc cạnh của nó từ A tới Z!

Khái Niệm Tâm Đối Xứng Của Đồ Thị

Đầu tiên, hãy cùng tìm hiểu tâm đối xứng là gì. Đơn giản thôi, tâm đối xứng của đồ thị hàm số là một điểm cố định mà khi các điểm trên đồ thị lấy đối xứng qua điểm này, chúng vẫn nằm trên đồ thị. Như kiểu bạn nhìn vào một bức tranh, khi gấp đôi lại theo trục điểm đó, cả hai bên đều khớp với nhau hoàn hảo.

Đặc điểm nổi bật

Khi nói đến tâm đối xứng, định nghĩa tâm đối xứng không thể bỏ qua việc nó có vai trò quan trọng trong hình học giải tích lẫn các ứng dụng thực tế như trong thiết kế kiến trúc và phân tích dữ liệu.

Cách Xác Định Tâm Đối Xứng Của Đồ Thị Hàm Số

Trước khi bạn muốn xác định tâm đối xứng của một hàm số, có một quy trình nhất định cần tuân theo. Hãy cùng đi sâu vào phần thú vị này.

Các bước cần thiết

Bắt đầu từ việc giả định tâm đối xứng là ( I(a, b) ). Tiếp theo, chúng ta tiến hành phép tịnh tiến trục tọa độ. Bước cuối cùng là thông qua các phép tính toán học để tìm ( a ) và ( b ).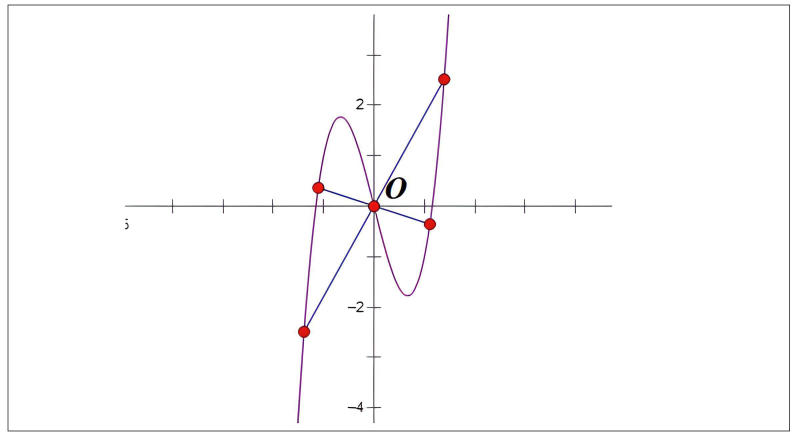

Ví dụ minh họa

Mình sẽ đưa ra một ví dụ để làm rõ hơn: Đối với hàm số bậc ba y = x^3 + 3x^2 – 9x + 1, khi tính toán, bạn sẽ tìm thấy tâm đối xứng ở điểm ((-1, 12)). Xem, không khó lắm nhỉ?

Tính Chất Đặc Trưng Và Vai Trò Của Tâm Đối Xứng

Tâm đối xứng có nhiều tính chất đặc trưng mà khi đã hiểu rõ, bạn sẽ thấy nó kì diệu ra sao.

Những đặc điểm riêng

Đối với hàm số lẻ, tâm đối xứng thường nằm ở gốc tọa độ ((0, 0)). Còn với hàm số bậc ba, điểm đó là chính điểm uốn. Điều này giúp chúng ta dễ dàng phân tích và khảo sát hình dạng đồ thị.

Ứng dụng sâu rộng

Tâm đối xứng giúp không chỉ trong toán học mà còn áp dụng vào phân tích dữ liệu, giúp bạn có cái nhìn toàn diện và logic hơn về dữ liệu cần xử lý.

Ứng Dụng Của Tâm Đối Xứng Trong Thực Tế

Các ứng dụng của tâm đối xứng thì thật sự rất phong phú và không ngờ tới. Từ giải pháp kiến trúc cho đến việc giải quyết bài toán tối ưu hóa, mọi nơi đều thấy dấu ấn của nó. Bạn có thể thử áp dụng để thấy sự khác biệt.

Kiến trúc và khoa học

Mình thấy rõ rằng trong kiến trúc, tính đối xứng không chỉ tạo ra sự hài hòa mà còn mang lại cái đẹp tuyệt vời cho công trình. Rồi đến các bài toán trong khoa học, tâm đối xứng có thể là mấu chốt giải quyết rất nhiều vấn đề phức tạp.

Các Phương Pháp Khác Để Phân Tích Đồ Thị Hàm Số

Ngoài việc xác định theo hướng tâm đối xứng, còn rất nhiều phương pháp khác để phân tích đồ thị. Đôi khi, đạo hàm bậc nhất và bậc hai được sử dụng để khảo sát và nghiên cứu sự chuyển đổi đồ thị.

Thách Thức Và Giải Pháp Khi Xác Định Tâm Đối Xứng

Dù biết rằng toán học có rất nhiều thách thức, nhưng mình sẽ cùng bạn vượt qua với các giải pháp hữu hiệu.

Khó khăn và cách giải quyết

Một số khó khăn phổ biến khi xác định tâm đối xứng bao gồm sự phức tạp trong phép tính và áp lực thời gian. Tuy nhiên, với việc luyện tập thường xuyên và chia nhỏ các bước, mọi thử thách đều có thể xử lý được.

Kết Luận

Tóm lại, tâm đối xứng không chỉ là một khái niệm toán học thú vị mà còn là một công cụ rất hữu dụng trong thực tế. Bạn đã có những thông tin cần thiết chưa? Nếu còn thắc mắc, đừng ngần ngại để lại comment hoặc chia sẻ bài viết này với bạn bè nhé. Hãy khám phá thêm tại mncatlinhdd.edu.vn!

Nguồn: http://mncatlinhdd.edu.vn/ Tác giả: Nguyễn Lân dũng