Phân Giác Tam Giác: Lý Thuyết, Ứng Dụng & Bài Tập (A-Z)

1. Kiến thức cần nhớ về đường phân giác trong tam giác

Định lý: Trong một tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy.

Ví dụ, xét tam giác (ABC) với (AD) là đường phân giác của góc (A) (D nằm trên cạnh BC). Theo định lý, ta có:

[frac{DB}{DC} = frac{AB}{AC}]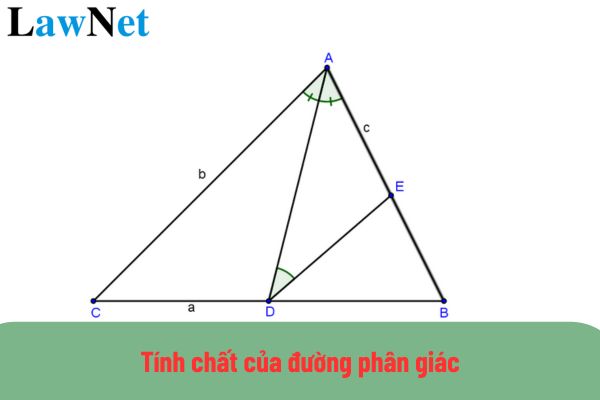

2. Đường phân giác ngoài của tam giác

Định lý: Tia phân giác của góc ngoài tại một đỉnh của tam giác chia cạnh đối diện thành hai đoạn tỉ lệ với hai cạnh kề của tam giác.

Chú ý: Định lý này mở rộng tính chất phân giác cho cả góc ngoài của tam giác.

Ví dụ: Cho tam giác (ABC) có (AE) là đường phân giác góc ngoài tại đỉnh (A) (E nằm trên tia đối của cạnh BC). Khi đó, ta có:

[frac{EB}{EC} = frac{AB}{AC}]

3. Các dạng toán thường gặp và phương pháp giải

Dạng 1: Tính độ dài cạnh, chu vi, diện tích

Phương pháp:

1. Sử dụng tính chất đường phân giác: Áp dụng định lý về đường phân giác trong và ngoài để thiết lập các tỉ lệ thức.
2. Biến đổi và tính toán: Dựa vào các tỉ lệ thức và thông tin đã cho để tìm ra các độ dài cần thiết.
3. Áp dụng công thức liên quan: Sử dụng các công thức tính chu vi, diện tích tam giác để hoàn thành bài toán.

Ví dụ:

Cho tam giác (ABC) có (AB = 5) cm, (AC = 7) cm, và (BC = 6) cm. (AD) là đường phân giác trong của góc (A). Tính độ dài (BD) và (DC).

Giải:

Áp dụng tính chất đường phân giác, ta có:

[frac{DB}{DC} = frac{AB}{AC} = frac{5}{7}]

Vì (DB + DC = BC = 6), ta có thể thiết lập hệ phương trình:

[begin{cases}frac{DB}{DC} = frac{5}{7} \DB + DC = 6end{cases}]

Giải hệ phương trình này, ta tìm được (DB = 2.5) cm và (DC = 3.5) cm.

Dạng 2: Chứng minh đẳng thức hình học và các bài toán khác

Phương pháp:

1. Sử dụng tính chất đường phân giác: Áp dụng định lý để thiết lập các tỉ lệ thức.
2. Biến đổi và suy luận: Sử dụng các tính chất hình học khác (ví dụ: tam giác đồng dạng, định lý Thales) để chứng minh các đẳng thức hoặc giải quyết các vấn đề liên quan.

4. Bài tập vận dụng

Để củng cố kiến thức, bạn có thể tham khảo và giải các bài tập sau:

• Bài 1: Cho tam giác (ABC) có (AB = 8) cm, (AC = 10) cm, và (BC = 12) cm. (AD) là đường phân giác trong của góc (A). Tính (BD) và (DC).
• Bài 2: Chứng minh rằng trong tam giác (ABC), nếu (AD) là đường phân giác của góc (A), thì tỉ số diện tích của tam giác (ABD) và tam giác (ACD) bằng tỉ số (AB/AC).

5. Kết luận

Hiểu rõ và biết cách áp dụng tính chất đường phân giác của tam giác là một kỹ năng quan trọng trong giải toán hình học. Việc nắm vững lý thuyết và thực hành giải các dạng bài tập khác nhau sẽ giúp bạn tự tin hơn khi đối mặt với các bài toán phức tạp.

Nguồn: https://mncatlinhdd.edu.vn/ Tác giả: Nguyễn Lân dũng