Khám Phá Hình Thoi Có 2 Đường Chéo Bằng Nhau Là Gì

Khám phá hình thoi có 2 đường chéo bằng nhau là hình gì

Khi nhắc đến hình học, đặc biệt là hình thoi, không ít người thắc mắc: Hình thoi có 2 đường chéo bằng nhau là hình gì? Để trả lời câu hỏi này, chúng ta cần tìm hiểu sâu về các tính chất hình học đặc biệt của hình thoi và mối quan hệ giữa hình thoi với các hình tứ giác khác, đặc biệt là hình vuông.

Tìm hiểu về tính chất hình học đặc biệt của hình thoi

Hình thoi nổi bật với các cạnh của nó đều bằng nhau. Đặc biệt, các đường chéo không chỉ giao nhau mà còn vuông góc và phân giác các góc trong hình. Tuy nhiên, một trong những điểm đặc biệt khiến nhiều người có thể lầm tưởng chính là tính chất hai đường chéo bằng nhau. Thực chất, trong hình thoi, hai đường chéo không bằng nhau. Chính đặc điểm này giúp phân biệt hình thoi với các loại tứ giác đặc biệt như hình vuông.

Hình vuông là một trường hợp đặc biệt của hình thoi, bởi vì ngoài việc có bốn cạnh đều nhau, nó còn có hai đường chéo bằng nhau và vuông góc tại trung điểm.

Khi bạn tìm hiểu kỹ về các tính chất hình thoi, bạn sẽ thấy, hai đường chéo sẽ không bao giờ bằng nhau trừ khi nó là hình vuông.

Làm thế nào để nhận biết một hình thoi dựa trên tính chất đường chéo

Nhận biết hình thoi không khó, nhưng để phân biệt với các tứ giác khác, đặc biệt là hình vuông, lại là thử thách. Với hình thoi, hai đường chéo không bằng nhau. Chúng giao nhau tại trung điểm mỗi đường và vuông góc. Ngược lại, hình vuông có hai đường chéo vừa bằng nhau vừa vuông góc, vừa làm phân giác cho các góc.

Một ví dụ điển hình

Hãy lấy một ví dụ: Bạn có một tứ giác với bốn cạnh bằng nhau. Nếu hai đường chéo bằng nhau, đó không phải là hình thoi mà là hình vuông. Điều này là chìa khóa để nhận biết sự khác biệt giữa hai hình này.

Hình vuông và mối quan hệ với hình thoi

Hiểu được hình vuông như một biến thể đặc biệt của hình thoi giúp chúng ta mở rộng tư duy hình học. Hình vuông, ngoài việc có các cạnh bằng nhau và đường chéo bằng nhau, còn có tất cả các góc là góc vuông, một điều mà hình thoi thông thường không có. 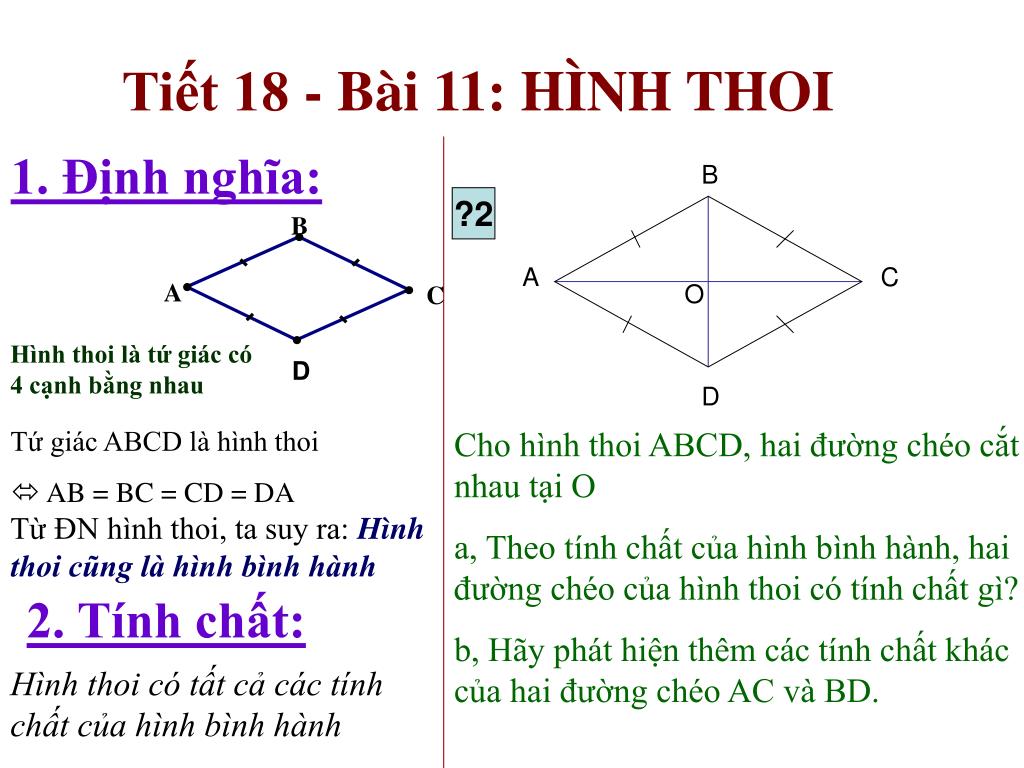Điều này tạo ra một sự liên kết mà đôi khi người học hình học dễ nhầm lẫn.

Phân tích các trường hợp đặc biệt và điều kiện riêng của hình vuông

Một khi ta nhận ra rằng hình vuông là một trường hợp đặc biệt trong tứ giác có tính chất của hình thoi, thì việc tìm hiểu sâu hơn về điều kiện để hình thoi chuyển thành hình vuông trở nên quan trọng.

Điều kiện chuyển đổi

Một tứ giác bốn cạnh đều có thể được coi là hình vuông nếu và chỉ nếu các góc bên trong đều là góc vuông. Điều này đồng nghĩa với việc hai đường chéo phải bằng nhau. Hình thoi chỉ trở thành hình vuông khi đáp ứng được điều kiện này.

Bài tập và ví dụ thực tiễn

Một số bài tập vận dụng

Để củng cố kiến thức về hình học và tính toán, hãy xem xét các bài tập về sự khác biệt giữa hình thoi và hình vuông. Ví dụ, khi cho rằng hai đường chéo có độ dài khác nhau, mời bạn: "Hãy chứng minh rằng tứ giác không phải là hình vuông dựa trên phân tích đường chéo."

Ví dụ minh họa

Hãy thử với ví dụ sau: Một hình thoi với bốn cạnh 5 cm. Nếu hai đường chéo là 6 cm và 8 cm, chứng minh rằng đó không phải là hình vuông. Phép tính đơn giản chủ yếu dựa trên độ dài của đường chéo để đưa ra kết luận.

Tại sao cần nắm vững lý thuyết về hình thoi và hình vuông

Việc hiểu rõ tính chất đặc biệt của hình thoi và hình vuông giúp bạn giải quyết bài toán nhanh chóng và hiệu quả hơn. Đặc biệt, nó giúp cải thiện tư duy lôgic và lập luận, thứ rất cần thiết trong nhiều khía cạnh cuộc sống và công việc.

Kết luận, việc nhận thức rõ về hình thoi và hình vuông không chỉ giúp bạn dễ dàng vượt qua các bài kiểm tra hình học mà còn mở ra cách nhìn rõ nét hơn trong các vấn đề thực tiễn. Nếu bạn có bất kỳ thắc mắc nào, đừng ngần ngại để lại bình luận hoặc chia sẻ để chúng ta cùng thảo luận thêm. Để khám phá thêm những kiến thức thú vị, mời bạn ghé thăm trang web mncatlinhdd.edu.vn.

Nguồn: http://mncatlinhdd.edu.vn/ Tác giả: Nguyễn Lân dũng