Table of Contents
I. Kiến thức cần nhớ
1. Định nghĩa đường cao của tam giác
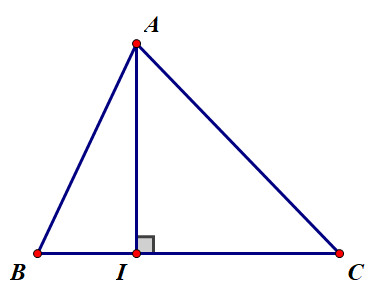
Đường cao của một tam giác là đoạn vuông góc kẻ từ một đỉnh đến đường thẳng chứa cạnh đối diện. Mỗi tam giác có ba đường cao.
2. Tính chất ba đường cao của tam giác
Ba đường cao của một tam giác luôn đồng quy tại một điểm. Điểm này được gọi là trực tâm của tam giác.

3. Tính chất đặc biệt của tam giác cân
Trong một tam giác cân, đường trung trực ứng với cạnh đáy cũng đồng thời là đường phân giác, đường trung tuyến và đường cao của tam giác đó.

Chứng minh:
Cho tam giác ABC cân tại A, đường cao AH. Xét hai tam giác vuông ABH và ACH:
- AB = AC (do tam giác ABC cân tại A)
- AH là cạnh chung
- góc AHB = góc AHC = 90 độ
=> Tam giác ABH = Tam giác ACH (cạnh huyền – cạnh góc vuông)
=> BH = CH (AH là đường trung tuyến)
=> góc BAH = góc CAH (AH là đường phân giác)
Vậy AH đồng thời là đường cao, đường trung tuyến và đường phân giác của tam giác ABC. Do AH vuông góc với BC tại H và BH = CH nên AH cũng là đường trung trực của BC.
Nhận xét:
Trong một tam giác, nếu có hai trong bốn loại đường (đường trung tuyến, đường phân giác, đường trung trực, đường cao) trùng nhau thì tam giác đó là tam giác cân.
4. Đặc biệt đối với tam giác đều
Trong một tam giác đều, trọng tâm, trực tâm, điểm cách đều ba đỉnh, điểm nằm trong tam giác và cách đều ba cạnh là bốn điểm trùng nhau.
II. Các dạng toán thường gặp
Dạng 1: Chứng minh hai đường thẳng vuông góc
Phương pháp: Sử dụng tính chất trực tâm của tam giác.
Nếu H là giao điểm của hai đường cao kẻ từ B và C của ΔABC thì AH ⊥ BC.
Ví dụ: Cho tam giác ABC có các đường cao BD và CE cắt nhau tại H. Chứng minh rằng AH vuông góc với BC.
Giải:
Vì H là giao điểm của hai đường cao BD và CE của tam giác ABC, nên H là trực tâm của tam giác ABC. Do đó, AH vuông góc với BC.
Dạng 2: Bài toán về đường cao với tam giác, tam giác cân, tam giác đều
Phương pháp:
- Sử dụng tính chất vuông góc của đường cao đối với cạnh đối diện.
- Sử dụng định lý “Trong một tam giác cân, đường cao ứng với cạnh đáy đồng thời là đường phân giác, đường trung tuyến, đường trung trực của tam giác đó” để một trong các đường trung tuyến, phân giác, đường cao, đường trung trực ứng với cạnh đáy cũng là các đường còn lại.
- Sử dụng nhận xét: Trong một tam giác, nếu có hai trong bốn loại đường (đường trung tuyến, đường phân giác, đường trung trực, đường cao) trùng nhau thì tam giác đó là tam giác cân.
Ví dụ: Cho tam giác ABC cân tại A, đường cao AH. Chứng minh rằng AH là đường trung tuyến, đường phân giác và đường trung trực của tam giác ABC.
Giải:
Vì tam giác ABC cân tại A và AH là đường cao ứng với cạnh đáy BC, theo tính chất của tam giác cân, AH đồng thời là đường trung tuyến, đường phân giác và đường trung trực của tam giác ABC.
Dạng 3: Chứng minh ba đường thẳng đồng quy
Phương pháp:
Nếu ba đường thẳng là ba đường cao của tam giác thì chúng cùng đi qua một điểm (trực tâm của tam giác).
Ví dụ: Cho tam giác ABC, gọi AD, BE, CF là ba đường cao. Chứng minh rằng ba đường thẳng AD, BE, CF đồng quy.
Giải:
Vì AD, BE, CF là ba đường cao của tam giác ABC, theo định lý về ba đường cao của tam giác, chúng đồng quy tại trực tâm của tam giác ABC.
Kết luận
Như vậy, trong tam giác cân, đường cao ứng với cạnh đáy đồng thời là đường trung tuyến, đường phân giác và đường trung trực của tam giác đó. Việc nắm vững kiến thức và các dạng toán liên quan đến đường cao sẽ giúp bạn giải quyết các bài toán hình học một cách hiệu quả.
Nguồn: https://mncatlinhdd.edu.vn/ Tác giả: Nguyễn Lân dũng
Giáo sư Nguyễn Lân Dũng là một trong những nhà khoa học hàng đầu Việt Nam trong lĩnh vực vi sinh vật học, với hơn 50 năm cống hiến cho giáo dục và nghiên cứu (Wiki). Ông là con trai của Nhà giáo Nhân dân Nguyễn Lân, xuất thân từ một gia đình nổi tiếng hiếu học. Trong sự nghiệp của mình, Giáo sư đã đảm nhiệm nhiều vị trí quan trọng như Chủ tịch Hội các ngành Sinh học Việt Nam, Đại biểu Quốc hội và được phong tặng danh hiệu Nhà giáo Nhân dân vào năm 2010.

